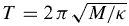Bewegungsgleichung
Die Bewegungsgleichung ist die Balance dreier Kräfte (ein Klick
auf sie zeigt mehr Details):
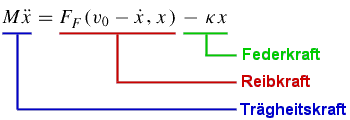
Die Trägheitskraft ist die
Masse des Blocks M multipliziert mit der Beschleunigung,
d.i. die zweite Ableitung der Position x(t) als
Funktion der Zeit t.
Die Federkraft ist durch
das Dehnen und Drücken der Feder verursacht. Sie ist proportional
zur Stärke dieses Dehnens bzw. Streckens. Dies ist das
Hooksche Gesetz. Der Proportionalitätsfaktor wird
Federkonstante 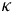 (der griechische Buchstabe kappa) genannt.
In der Animation wird die Federkraft als grüner Pfeil dargestellt.
(der griechische Buchstabe kappa) genannt.
In der Animation wird die Federkraft als grüner Pfeil dargestellt.
Die Reibkraft ist die Folge
der Wechselwirkung zwischen dem Block und der Oberfläche des
Förderbandes (welches sich mit der konstanten Geschwindigkeit
v0 bewegt). In der Animation wird diese Kraft
als roter bzw. oranger Pfeil gezeigt. Darüberhinaus zeigt ein
roter Balken die dissipierte Energie pro Zeiteinheit.
Die Reibkraft ist im allgemeinen ein Funktion vieler Variablen:
Der relativen Gleitgeschwindigkeit
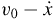 ,
der Position, der Kraft, der Vergangenheit etc. Die
Komplexität der Wechselwirkung zwischen den Oberflächen zweier
fester Körper ist das zentrale Thema des Friction Lab.
In der Animation wurden zwei verschiedene Funktionen, d.h.
Reibungsgesetze, gewählt:
Das Coulomb'sche Gesetz
und die viskose Reibung.
,
der Position, der Kraft, der Vergangenheit etc. Die
Komplexität der Wechselwirkung zwischen den Oberflächen zweier
fester Körper ist das zentrale Thema des Friction Lab.
In der Animation wurden zwei verschiedene Funktionen, d.h.
Reibungsgesetze, gewählt:
Das Coulomb'sche Gesetz
und die viskose Reibung.
Ohne Reibung bekommen wir die Bewegungsgleichung eines
so genannten harmonischen Oszillators. Die Bewegung des
Blocks wird sinusförmig mit konstanter Amplitude.
Die Oszillationsperiode T ist unabhängig von der
Oszillationsamplitude. Sie ist durch die Masse und die
Federkonstante bestimmt:
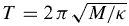
In der Animation bekommt man diese Bewegung, in dem man alle
Reibungsparameter (mu_s und mu_k im Fall des Coulomb'schen Gesetz
bzw. gamma im Fall der viskosen Reibung) auf Null setzt.
The Friction Lab© 2001, e-mail:
Franz-Josef doht Elmer aht unibas doht ch,
last modified: 2001/11/25


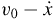 ,
der Position, der Kraft, der Vergangenheit etc. Die
Komplexität der Wechselwirkung zwischen den Oberflächen zweier
fester Körper ist das zentrale Thema des Friction Lab.
In der Animation wurden zwei verschiedene Funktionen, d.h.
Reibungsgesetze, gewählt:
Das Coulomb'sche Gesetz
und die viskose Reibung.
,
der Position, der Kraft, der Vergangenheit etc. Die
Komplexität der Wechselwirkung zwischen den Oberflächen zweier
fester Körper ist das zentrale Thema des Friction Lab.
In der Animation wurden zwei verschiedene Funktionen, d.h.
Reibungsgesetze, gewählt:
Das Coulomb'sche Gesetz
und die viskose Reibung.