Home Dr. Franz-Josef Elmer

Solid-Solid Friction

Self-organized criticality (SOC)

I am investigating simple mechanical models which are relevant for dry friction (i.e., Frenkel-Kontorova model, Frenkel-Kontorova-Tomlinson model, Burridge-Knopoff model, train model). Some of this models show self-organized criticality (SOC). Results concerning the Frenkel-Kontorova model are published in Ref. 12, 18, and 21. I have also investigated a Frenkel-Kontorova-like model which may be relevant for Barkhausen noise (see Ref. 11 and 19). In Ref. 22 I gave a review on SOC in dry friction concerning these models as well as experiments. 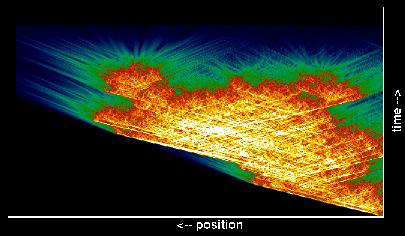Recently I found that SOC with superposed log-periodicities in the avalanche statistics occurs in the train model for a certain type of friction law (see Ref. 32).

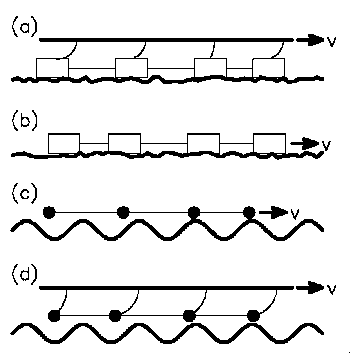
SOC models Several mechanic models showing power laws in the avalanche statistics: (a) Burridge-Knopoff (earthquake) model, (b) train model, (c) Frenkel-Kontorova model, and (d) Frenkel-Kontorova-Tomlinson model. Neigboring blocks or particles are coupled by springs. In model (b) and (c) the right end of the chain is pulled very slowly, whereas is case (a) and (d) a rigid plate is pulled. The chain is connected at the plate by leaf springs. In the first two models the interaction with the surface is modeled by a phenomenological friction law. For the two other models, this law is replaced by a spatially periodic potential and viscous friction. Model (b) and (c) show real SOC, whereas the two other models have an intrinsic cutoff where the power-law regime ends. The cutoff scales with the inverse of the square root of stiffness of the leaf springs. For more details see Ref. 22.
avalanche An avalanche in the Frenkel-Kontorova model. The avalanche starts on the right hand side at the pulled particle. There is a shock wave propagating to the left. The color codes the kinetic energy of the particles. For more details see Ref.  18.

Home Back to my home page