The Lab The Lecture Room The Equations of Motion Oscillations and Resonances Nonlinear Dynamics Miscellaneous Topics Links and Literature The Harmonic Oscillator Nonlinear Oscillations Nonlinear Resonance Parametric Resonance

Nonlinear Oscillations

A pendulum is properly modelled by a harmonic oscillator only for small angles of elongation. Maybe you have observed in the lab that the period of oscillation increases with increasing amplitude of oscillation. Starting near the upside-down position, you will find that the period becomes much larger than for small-angle oscillations. In fact, the period approaches infinity in the limit _max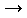180°. In the virtual lab (and in reality too) you will never reach this limit.

Even though the equation of motion of an undamped and undriven pendulum is nonlinear, one can calculate its frequency as a function of the amplitude _max. In order to solve this nonlinear differential equation

(1)	d2/dt2 + 02sin = 0,

notice that the total energy

(2)	E = ½(d/dt)2 - 02cos

is a constant during the motion of the pendulum. In the maximum elongation _max, the kinetic energy is zero. Thus,

(3)	E = -02cosmax.

Solving (2) for d/dt leads to

d/dt = ±[2(E+₀²cos)]^1/2.

This first-order differential equation can be solved by separating the independent variable t from the dependent one . That is, deal with the differential quotient as if it would be a real quotient d divided by dt. Then, put all terms with on the left-hand side of the equation and all terms with t on the right-hand side:

d/[2(E + ₀²cos)]^1/2 = ±dt.

To get the period of oscillations, integrate over a half cycle

Because the integrand on the left-hand side is an even function in , you will get

(4)

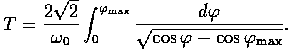
Note that E has been replaced by (3).

This integral can not be expressed by elementary functions like polynomials or trigonometric functions. This is possible only in the limit of _max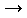0, where the cosine function can be approximated by a Taylor series. Taking only the first and the second term, you will get an elementary integral leading to the well-known result of T = 2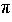/₀. For an arbitrary value of _max, the integral of (4) defines a so-called complete elliptic integral. It sounds like a naïve trick to give an unsolvable integral a name. Indeed, it is a trick but a fruitful one because elliptic integrals appear quit often in mathematics and physics. Not as often as trigonometric functions of course, but often enough to give them a name, to find out their mathematical properties, to tabulate their values, and to include them into standard mathematical subroutine packages on computers. One distinguishes three different types of elliptic integrals. The second one is related to the circumference of an ellipse, that's why the name. In our case, the first one is relevant. The substitution x =  sin(/2)/sin(_max/2) turns (4) into the canonical form of the complete elliptic integral of the first kind K

(5)

Here are a few properties of K(): K(0) = /2, K(/2)  , K() = /2(1+2/4+...). Thus, in the limit max0, T approaches to T0=2/0, i.e., the result of the harmonic oscillator. The plot shows the ratio T/T0. Try to verify this curve by measurements! Go into the lab and measure the period of oscillation of the undamped and undriven pendulum with the stopwatch.

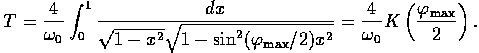
QUESTIONS worth to think about:

What is the reason for a diverging period of oscillations? Can you calculate analytically the solution of (1) in that limit? Can you find other nonlinear oscillators with diverging periods? What happens if the energy is larger than -02cosmax?

previous	top	next

© 1998 Franz-Josef Elmer,  Franz-Josef doht Elmer aht unibas doht ch, last modified Monday, July 20, 1998.