|
|
|
In linear dynamics, one seeks the fundamental solutions from which one can build all other solutions. In nonlinear dynamics, the main questions are: What is the qualitative behavior of the system? Which and how many non-wandering sets (i.e. a fixed point, a limit cycle, a quasi-periodic or chaotic orbit) occur? Which of them are stable? How does the number of non-wandering sets change while changing a parameter of the system (called control parameter)? The appearance and disappearance of a non-wandering set is called a bifurcation. Change of stability and bifurcation always coincide. There are the two different sides of the same medal!
A non-wandering set may be stable or unstable. There are two types of stability, a weaker and a stronger one:
Thus, a non-wandering set is either asymptotically stable, marginally stable (i.e. only Lyapunov stable), or unstable. Asymptotically stable non-wandering sets are also called attractors. The basin of attraction is the set of all initial states approaching the attractor in the long time limit.
How can we check the stability of a non-wandering set? There is a scheme called linear
stability analysis: Assuming u0(t) is the orbit
you want to check whether it is stable or not.
It is asymptotically stable if any infinitesimal small perturbations
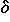 u
decays. Thus, make the ansatz
u
decays. Thus, make the ansatz 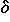 u,
u,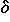 u.
You will get
u.
You will get
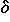 u/dt = DF(u0)
u/dt = DF(u0)
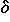 u
u
and
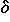 un+1 = DF(u0)
un+1 = DF(u0)
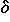 un,
un,
respectively. These linear equations of motion are justified as long as the orbit doesn't go
too far away from ![]() st)
st)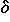 us
us![]() s)n
s)n us
us![]() s
s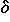 us
us![]() s are the roots of the characteristic
polynomial det(DF(u0)-
s are the roots of the characteristic
polynomial det(DF(u0)-![]() )=0. The fixed point u0 is asymptotically
stable if all eigenvalues
)=0. The fixed point u0 is asymptotically
stable if all eigenvalues ![]() s are inside a stability area of the complex plane.
In the time-continuous case, this stability area is the half-plane left of the imaginary axis,
whereas in the time-discrete case it is the unit circle around the origin.
If at least one eigenvalue is outside the stability area the corresponding
fundamental solution would increase exponentially. Thus, the fixed point will be unstable.
If an eigenvalue is just on the border of stability, you can not decide by linear stability analysis whether the fixed point is unstable, asymptotically
or marginally stable.
s are inside a stability area of the complex plane.
In the time-continuous case, this stability area is the half-plane left of the imaginary axis,
whereas in the time-discrete case it is the unit circle around the origin.
If at least one eigenvalue is outside the stability area the corresponding
fundamental solution would increase exponentially. Thus, the fixed point will be unstable.
If an eigenvalue is just on the border of stability, you can not decide by linear stability analysis whether the fixed point is unstable, asymptotically
or marginally stable.
Calculating the roots of a polynomial analytically is impossible if its order is greater than five, and tedious if the order is greater than two. For time-continuous system, the question on stability can be answered without explicitely calculating the eigenvalues, thanks to the theorem of Routh and Hurwitz. This theorem says that the real parts of all roots of a polynomial are negative if and only if certain conditions are fulfilled which can be easily calculated. This theorem is useful even in the case of a two-dimensional phase space where the characteristic polynomial is quadratic: Both eigenvalues have negative real part if and only if the determinant DF(u0) is positive and the trace of DF(u0) is negative. The figure below shows a classification scheme of the fixed points of two-dimensional phase spaces.
The notion spiral and node are inspired by the flow near the fixed point. A pair of conjugated complex
eigenvalues lead to a spiral, whereas a node is causes by two real eigenvalues of the same sign. Real eigenvalues
of different sign lead to a saddle. In general, a saddle is a fixed point where at least one eigenvalue has
a positive real part but also at least one eigenvalue has a negative real part. Near a saddle, an orbit is usually
attracted at first but repelled later on. There are points in the phase space which approach the fixed point for
t ![]()
 . They form the stable manifold.
The eigenspace for the eigenvalues with negative real part is tangential to the stable manifold. The unstable
manifold are built by all points approaching the fixed point for t
. They form the stable manifold.
The eigenspace for the eigenvalues with negative real part is tangential to the stable manifold. The unstable
manifold are built by all points approaching the fixed point for t ![]() -
-  . Saddles and their stable manifolds are usually the boundaries of a basin of attraction. The undriven
pendulum has a saddle point (corresponding to the upside-down equilibrium position) and a spiral if
. Saddles and their stable manifolds are usually the boundaries of a basin of attraction. The undriven
pendulum has a saddle point (corresponding to the upside-down equilibrium position) and a spiral if ![]() < 2
< 2![]() 0 or a node if
0 or a node if ![]() > 2
> 2![]() 0 (see the flow
on the previous page).
0 (see the flow
on the previous page).
The number of attractors in a nonlinear dynamical system can change when a system parameter is changed. This change is called bifurcation. It is accompanied by a change of the stability of an attractor. In a bifurcation point, at least one eigenvalue of the Jacobian gets a zero real part. There are three generic types of so-called co-dimension-one bifurcations (the term codimension counts the number of control parameters for which fine tuning is necessary to get such a bifurcation):
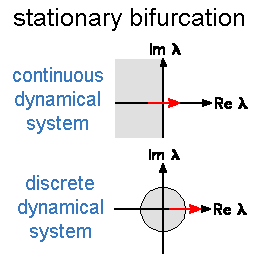 In a stationary
bifurcation, a single real eigenvalue crosses the boundary of stability.
In the Pendulum Lab, stationary bifurcations of limit cycles occur quit
often. They are stationary bifuractions of fixed points in a discrete dynamical system because limit cycles are
fixed points in the Poincaré map. In a stationary
bifurcation, a single real eigenvalue crosses the boundary of stability.
In the Pendulum Lab, stationary bifurcations of limit cycles occur quit
often. They are stationary bifuractions of fixed points in a discrete dynamical system because limit cycles are
fixed points in the Poincaré map. |
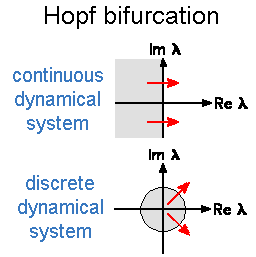 Hopf bifurcations
occur when a conjugated complex pair crosses the boundary of stability. In the time-continuous case, a limit
cycle bifurcates. It has an angular frequency which is given by the imaginary part of the crossing pair. In the
discrete case, the bifurcating orbit is generally quasiperiodic, except that the argument of the crossing pair times
an integer gives just 2 Hopf bifurcations
occur when a conjugated complex pair crosses the boundary of stability. In the time-continuous case, a limit
cycle bifurcates. It has an angular frequency which is given by the imaginary part of the crossing pair. In the
discrete case, the bifurcating orbit is generally quasiperiodic, except that the argument of the crossing pair times
an integer gives just 2 |
 In discrete
dynamical systems, a certain bifurcation is possible which is absent in continuous systems: The period doubling bifurcation.
Here, a real eigenvalue crosses the boundary of stability at -1. In a period-doubling bifurcation point, a period-2
orbit bifurcates. You can find this type of bifurcation quite often in the Pendulum Lab. In discrete
dynamical systems, a certain bifurcation is possible which is absent in continuous systems: The period doubling bifurcation.
Here, a real eigenvalue crosses the boundary of stability at -1. In a period-doubling bifurcation point, a period-2
orbit bifurcates. You can find this type of bifurcation quite often in the Pendulum Lab. |
Crossing the boundary of stability only indicates a bifurcation point and the type of the bifurcating solutions. But it doesn't tell you how and how many new solutions bifurcate or disappear in a bifurcation point. To answer this question one has to take into account the leading nonlinear terms. This might appear to be a difficult task. But fortunately, a theorem and a transformation help us simplifying this analysis:
Below, the main normal forms (for continuous dynamical systems) of stationary co-dimension-one bifurcations are
shown. The phase space variable is u. The control parameter is
![]() .
The bifurcation point is at
.
The bifurcation point is at ![]() = 0.
The direction of motion in the one-dimensional phase space is shown by arrows. Stable (unstable) fixed points are
drawn as red solid (dotted) lines. The normal forms are shown in blue.
= 0.
The direction of motion in the one-dimensional phase space is shown by arrows. Stable (unstable) fixed points are
drawn as red solid (dotted) lines. The normal forms are shown in blue.
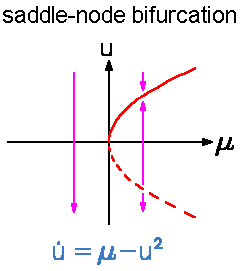 The generic case of stationary co-dimension-one
bifurcation is a saddle-node bifurcation. It is generic (that is, the probability is finite to pick
a dynamical system having a saddle-node bifurcation) because fixed points lie on a smooth one-dimensional manifold
in the combined space of phase space and control parameter. The minima and maxima of The generic case of stationary co-dimension-one
bifurcation is a saddle-node bifurcation. It is generic (that is, the probability is finite to pick
a dynamical system having a saddle-node bifurcation) because fixed points lie on a smooth one-dimensional manifold
in the combined space of phase space and control parameter. The minima and maxima of |
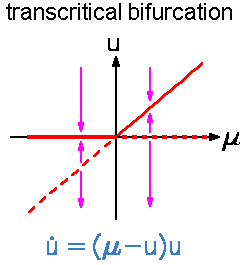 The transcritical
bifurcation occurs when in the combined space of phase space and
controlparameter space two different manifolds of fixed points cross each
other. At the crossing point the fixed points exchange there stability property. That is, the unstable fixed point
becomes stable and vice versa. Note, that beyond the bifurcation point the number of fixed points has not changed
contrary to saddle-node bifurcation where two fixed points appear or disappear. A transcritical
bifurcation is not a generic bifurcation in a phase space with more than one dimension because it is unlikely that
two lines cross each other in a space with more than two dimensions. The transcritical
bifurcation occurs when in the combined space of phase space and
controlparameter space two different manifolds of fixed points cross each
other. At the crossing point the fixed points exchange there stability property. That is, the unstable fixed point
becomes stable and vice versa. Note, that beyond the bifurcation point the number of fixed points has not changed
contrary to saddle-node bifurcation where two fixed points appear or disappear. A transcritical
bifurcation is not a generic bifurcation in a phase space with more than one dimension because it is unlikely that
two lines cross each other in a space with more than two dimensions. |
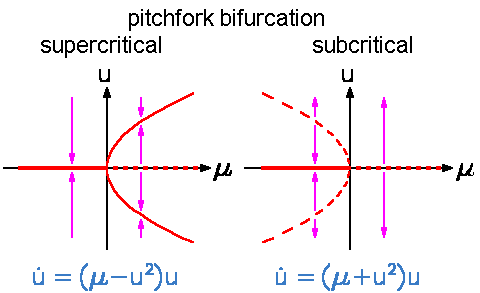 Pitchfork bifurcations are possible in dynamical
systems with an inversion or reflection symmetry.
That is, an equation of motion that remains
unchanged if one changes the sign of all phase space variables (or at least for one). An example is the undriven
pendulum. Usually, such a system has a symmetric fixed point (or limit cycle). Pitchfork bifurcations are the
generic bifurcations when such a symmetric solution changes its stability. The bifurcating solution does not have
the full symmetry of the equation of motion. This phenomenon is called broken symmetry. A solution with a broken
symmetry does not occur in isolation because the broken symmetry applied onto such a solution generates a new solution where
the same symmetry is broken. All such solutions build a family. Therefore, always two fixed
points with a broken symmetry bifurcate at once in a pitchfork bifurcation. Both are either stable (supercritical pitchfork
bifurcation) or unstable (subcritical pitchfork bifurcation). Pitchfork bifurcations are possible in dynamical
systems with an inversion or reflection symmetry.
That is, an equation of motion that remains
unchanged if one changes the sign of all phase space variables (or at least for one). An example is the undriven
pendulum. Usually, such a system has a symmetric fixed point (or limit cycle). Pitchfork bifurcations are the
generic bifurcations when such a symmetric solution changes its stability. The bifurcating solution does not have
the full symmetry of the equation of motion. This phenomenon is called broken symmetry. A solution with a broken
symmetry does not occur in isolation because the broken symmetry applied onto such a solution generates a new solution where
the same symmetry is broken. All such solutions build a family. Therefore, always two fixed
points with a broken symmetry bifurcate at once in a pitchfork bifurcation. Both are either stable (supercritical pitchfork
bifurcation) or unstable (subcritical pitchfork bifurcation).In the Pendulum Lab, pitchfork bifurcations of limit cycles occur quite often. As an example, try the following experiment: Shake a horizontally driven pendulum faster than its eigen frequency. It will show a tiny oscillation around the equilibrium value |
The bifurcation diagrams of a Hopf and a period doubling bifurcation are similar to the diagram of a pitchfork bifurcation. That is, the bifurcating periodic or quasiperiodic solution is either stable (supercritical bifurcation) or unstable (subcritical bifurcation). Again, a broken symmetry is responsible for this similarity. Here, it is the invariance of the dynamical system against translations in time.
| QUESTIONS worth to think about: |
|