|
|
|
Nonlinear dynamics is a language to talk about dynamical systems. Here, brief definitions are given for the basic terms of this language. All these terms will be illustrated at the pendulum.
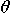 is also needed
because the pendulum becomes a nonautonomous system.
In spatially extended systems, the state is often a field (a scalar
field or a vector field). Mathematically spoken, fields are functions with space
coordinates as independent variables. The velocity field of a fluid is a well-known example.
is also needed
because the pendulum becomes a nonautonomous system.
In spatially extended systems, the state is often a field (a scalar
field or a vector field). Mathematically spoken, fields are functions with space
coordinates as independent variables. The velocity field of a fluid is a well-known example.
|
|
|
|
 .
Its dynamics reads
.
Its dynamics reads  /dt = 1,
/dt = 1, n+1 =
n+1 =  n,
depending on whether time is continuous or discrete.
For the periodically driven pendula, it is also natural to take the
driving phase
n,
depending on whether time is continuous or discrete.
For the periodically driven pendula, it is also natural to take the
driving phase 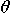 as the new state variable.
Its equation of motion reads
as the new state variable.
Its equation of motion reads
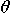 /dt = 2 /dt = 2 |
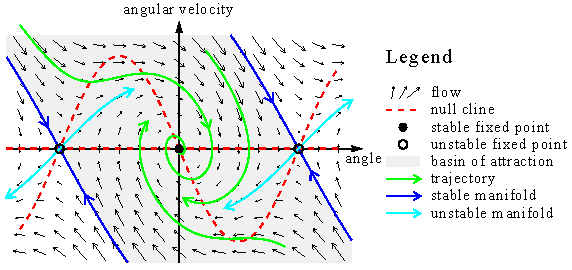 As an example, the figure shows the flow of a damped pendulum.
The black arrows of the vector field F are tangential at the
trajectories.
In a two-dimensional phase space, you can draw a qualitative
picture of the flow and the orbits. First, draw the so-called null clines.
These are the lines were the time derivative
of one component of the state variable is zero.
Here, one null cline is the angle axes because the time derivative of the angle is
zero when the angular velocity is zero.
The other null cline is
As an example, the figure shows the flow of a damped pendulum.
The black arrows of the vector field F are tangential at the
trajectories.
In a two-dimensional phase space, you can draw a qualitative
picture of the flow and the orbits. First, draw the so-called null clines.
These are the lines were the time derivative
of one component of the state variable is zero.
Here, one null cline is the angle axes because the time derivative of the angle is
zero when the angular velocity is zero.
The other null cline is 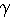 . . |
 A carefully chosen (curved) plane in the phase space that is crossed
by almost all orbits.
It is a tool developed by Henri Poincaré (1854-1912) for a visualization
of the flow in a phase space of more than
two dimensions. The Poincaré section has one dimension less than the phase space.
The Poincaré map maps the points of the Poincaré
section onto itself. It relates two consecutive intersection points.
Note, that only those intersection points counts which come
from the same side of the plane.
A Poincaré map turns a continuous dynamical system
into a discrete one.
If the Poincaré section is carefully chosen no information is lost concerning
the qualitative behavior of the dynamics.
Poincaré maps are invertable maps because one gets un
from un+1 by following the orbit backwards.
In the Pendulum Lab, you can turn the
oscilloscope into a special Poincaré map called
stroboscopic map were the Poincaré section is defined by a certain
phase of the time-periodic driving.
A carefully chosen (curved) plane in the phase space that is crossed
by almost all orbits.
It is a tool developed by Henri Poincaré (1854-1912) for a visualization
of the flow in a phase space of more than
two dimensions. The Poincaré section has one dimension less than the phase space.
The Poincaré map maps the points of the Poincaré
section onto itself. It relates two consecutive intersection points.
Note, that only those intersection points counts which come
from the same side of the plane.
A Poincaré map turns a continuous dynamical system
into a discrete one.
If the Poincaré section is carefully chosen no information is lost concerning
the qualitative behavior of the dynamics.
Poincaré maps are invertable maps because one gets un
from un+1 by following the orbit backwards.
In the Pendulum Lab, you can turn the
oscilloscope into a special Poincaré map called
stroboscopic map were the Poincaré section is defined by a certain
phase of the time-periodic driving.
|