|
|
 |
 |
 |
 |
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
While you played with the driven pendula in the lab, you may have discovered that it can behave very erratic. For example, you may have noticed irregular sequences of left and right turns. This behavior, called deterministic chaos, is the most prominent effect of nonlinear dynamics. The term "deterministic chaos" seems to be a contradiction in itself. How can something be deterministic and chaotic at the same time?
A key element of deterministic chaos is the sensitive dependence of the
trajectory on the initial conditions.
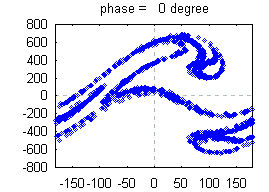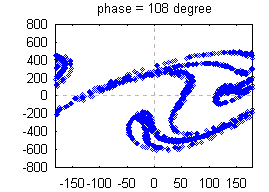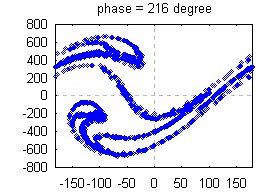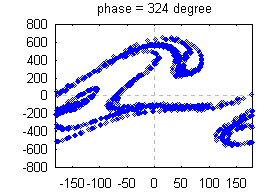
As an example, the plot on the left shows the first 15 seconds of a
demonstration of this effect for a horizontally driven pendulum.
The initial conditions are How predictable is a chaotic system? As any deterministic system, it is predictable on a short time scale. But on a long time scale, chaotic systems become unpredictable. They behave seemingly irregular. It is this very behavior why such systems are called "chaotic". Predictability is lost at a time, called prediction horizon, that depends only logarithmically on the uncertaincy of the initial conditions. Thus, the prediction horizon increases fairly slowly with increasing knowledge of the initial condition. There is an ultimate prediction horizon because the error of the initial condition can not be smaller than the unavoidable thermal noise. We can not foresee the future beyond this horizon! It depends on the system how far away this horizon actually is. For the example shown in the plot, it is about 8 seconds. For the weather, it may be roughly 10 days (maybe in places like southern California it can be quite longer). And for the our solar system with all planets, the prediction horizon lies very far in the future, namely, a few million years (luckily, otherwise astronomy wouldn't be the paradigma of successful predictions). |
 How can we understand
deterministic chaos? Note, that sensitivity on the initial conditions isn't a privilege of nonlinear dynamics.
It also happens in linear systems! For example, take the following time-discrete dynamical systemThe distance between two different solutions increases by the factor two in each time step. But of course, this is not deterministic chaos! It is a kind of explosion (like the population explosion!). Sensitivity on the initial conditions leads to chaos only if the trajectories are bound. That is, the system can not blow up to infinity. With linear dynamics, you can have either sensitivity on the initial conditions or bound trajectories, but not both. With nonlinearities, you can have both. The figure shows why this is possible. Imagine the phase space is a piece of dough from which you want to make flaky pastry for croissants: You roll it out and fold it. Usually you repeat this step a few times. Suppose at the beginning two poppy-seeds are located next to each other. Each time the dough is rolled out the distance between the seeds increases. Eventually, this increase is stopped when the seeds are on different sides of the folding line. At that moment the distance changes unpredictable. Assuming an initial distance of 1 mm and a piece of dough which is 10 cm long, you reach the prediction horizon after only seven rolling-folding steps. Thus, stretching and folding are responsible for deterministic chaos. And there is no folding without nonlinearities! |
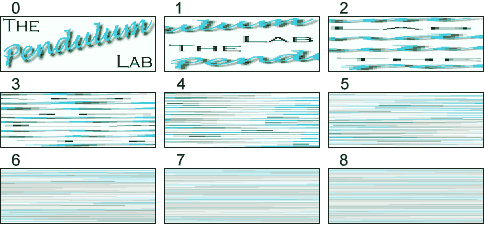 There is a
simple map on a two-dimensional phase space, called baker map, which is an abstract version of making flaky
pastry: (xn-1/2)/2,where is the step
function which is 1 for positive arguments and zero otherwise. The baker map is a piecewise linear map of the unity
square onto itself. First, the square is stretch in the x direction by the factor two and squeezed in the
y direction also by the factor two. In the second step, the stretched and squeezed square is cut in the middle
and the right half is put onto the left half. This corresponds to the folding step. Note, that the map preserves
the size of an area during mapping. The sequence of pictures shows the mixing properties of the baker map when it is applied to the
logo of the pendulum lab. |
 This animation of a
horizontal pendulum (with the same parameters as above) shows how the phase space is stretched and fold during
one cycle of driving. Contrary to the baker map the phase space shrinks because of dissipation. This animation
was produced by calculating the orbits of 1600 initial conditions which are distributed uniformly over the visible
phase space. After a transient the initial rectangle shrinks neither to a point nor a line but to something which
is called a strange attractor. It has a structure similar to flaky pastry. After each cycle the number of leaves
is increased by some factor. Thus, in the longtime limit the strange attractor has infinitely many leaves (click on
here for having a look at these details). Nevertheless,
the volume in phase space is zero! Such a geometric object is indeed strange. But nowadays, it is well-known
as fractals. |
| QUESTIONS worth to think about: |
|
|
|
|
|
Franz-Josef doht Elmer aht unibas doht ch,
last modified Sunday, July 26, 1998.
= 1/sec, 
= -140°,
