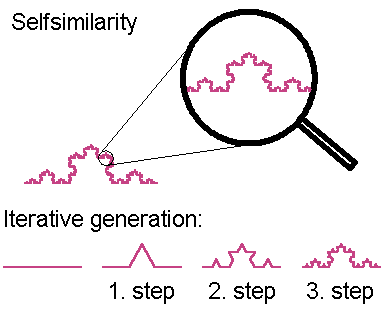Fractals

A fractal is a geometric object which looks similar to itself under a magnifying glass. This selfsimilarity is a property which is very well illustrated by the Koch curve or snow flake curve. As it is shown in figure, it is generated by an iterative process. Even though the Koch curve is bound (i.e., you can draw a circle with finite radius around it), its length is infinite. Of course, if your magnifying glass has only finite resolution, the curve has finite length. That is, if you measure the length with a ruler of finite length l, you will find that the length L of the Koch curve is also finite. But if you take a smaller ruler, you will see more details leading to a greater length. Thus, L is a decreasing function of l. How does it depend on l? Imagine you have a set of rulers. The biggest one just spans from one end of the Koch curve to the other one. It defines the length unit. The second largest ruler is just one third of the biggest one. The third largest ruler is one third of the second largest, etc. How long is the Koch curve measured with nth largest ruler? It is just the length of the nth iterate. Thus, the length of the Koch curve measured with the second largest ruler is four times the length of the second largest ruler, i.e., 4/3. Here is a table with the results for other iterates: number of iterations: 0 1 2 ... n ... ruler length l: 1 1/3 1/9 ... 1/3n ... curve length L: 1 4l = 4/3 16l = 16/9 ... 4nl = (4/3)n ...

Thus, the length L of the Koch curve diverges for l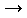0 like a power law, i.e.,

where D = ln 4/ln 3 = 1.2618... is the so-called fractal dimension of the curve. It is a generalization of the Euclidian dimension which has only nonnegative integer values. A fractal dimension can be any fractional or real number, that's why the name. The fractal dimension of a nonfractal object is identical with its Euclidian dimension. A fractal is an object with a fractal dimension different from its Euclidian dimension.

Kneading the phase space in a dissipative dynamical system leads to a non-wandering set which is also a fractal. It is called a strange attractor if it is an asymptotically stable set. The figure below shows the strange attractor of the horizontally driven pendulum. The sequence of blow-ups clearly shows its fractal nature.

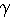g = 9.81 m/sec², l = 1 m, = 1/sec, a = 0.85 m, f = 1 Hz.

QUESTIONS worth to think about:

Is it possible to construct in an iterative way a bound curve with fractal dimension two? A Cantor set is a fractal constructed similarly to the Koch curve: Start with a finite line and take away one third in the middle. You get two lines with a length of one third of the original line. Proceed with both lines as with the original line. Do this infinitely often with all lines. What is the fractal dimension of the Cantor set? Is the non-wandering set of the baker map a fractal? Can you slightly modify the baker map in such a way that its strange attractor has a fractal dimension you can freely choose?

previous	top	next

© 1998 Franz-Josef Elmer,  Franz-Josef doht Elmer aht unibas doht ch, last modified Sunday, April 14, 2002.